用于情感分析的LSTM网络(LSTM Networks for Sentiment Analysis)

发表于 | 更新于 | 评论数：
原文

声明：

  1. 本译文并未取得原作者授权，如有侵权行为，请发邮件到13581561959@163.com。我将立即删除。
  2. 翻译中，意译的地方较多。如有错误，或不准确的地方，欢迎邮件讨论，谢谢。

这个教程旨在演示如何使用Theano实现一个基于长短期记忆的循环神经网络。在这里，该模型用于分析最大的影视评论数据集（即IMDB数据集）中的影评中的情感色彩。

在这个教程中，我们将训练一个二分分类的模型。对于给定一个影评，该模型会判断其是积极还是消极的。

数据

上面已经提到了，本文的python脚本被用于在一个很大的影评数据集上训练长短期记忆循环神经网络模型。

虽然数据是公开的，但是本文作者提供一个已经按照LSTM实现的要求预先处理过的数据集。运行本文提供的代码将自动下载这些数据。如果你想使用自己的数据来训练模型，请使用本文提供的数据预处理脚本对数据进行清洗。

一旦模型被训练完成后，你就能使用你自己的基于本文提供的字典的语料库测试它。

模型

LSTM

在传统的循环神经网络中，在梯度后向传播的过程中，经过大量（与步长一样多）的与循环隐藏层相关联的权重矩阵相乘，梯度向量达到最优。（In a traditional recurrent neural network, during the gradient back-propagation phase, the gradient signal can end up being multiplied a large number of times (as many as the number of timesteps) by the weight matrix associated with the connections between the neurons of the recurrent hidden layer. ）这意味着，转置矩阵的维度对于学习的过程影响很大。

如果这个矩阵的权重比较小（或者说，更规范地说，如果权重矩阵的特征值小于1.0），这将导致一种被称为梯度消失的情况发生，即梯度向量太小了以至于学习的过程变得缓慢或停止。在这种情况下，学习数据间的长短期关系的也非常的困难。与之相对，如果这个矩阵的权重非常的大（或者，更规范地说，如果权重矩阵的主特征值大于1.0），这会导致梯度向量太大以至于学习出现偏离。这通常被称为梯度膨胀。（译者，这是再说过拟合和欠拟合吗？）

LSTM通过一个全新的结构，记忆元（见图1），来解决这些问题。一个记忆元由四个主要的元素构成：一个输入门，一个自反馈的神经元，一个失忆门和一个输出门。自反馈神经元的自反馈连接的权重为1.0，并且其屏蔽任何的外部干扰，确保记忆元的状态稳定当其从一个时间点转移到下一个时间点。这些门被用来模拟记忆元与自己和外部环境交互。输入门能允许输入信号改变其状态或阻止它。另一方面，输出门能允许或阻止记忆元的状态影响其他的神经元。最后，失忆门能模拟记忆元的自反馈连接，根据需要，记忆元可以选择记住或忘记它的上一个状态。

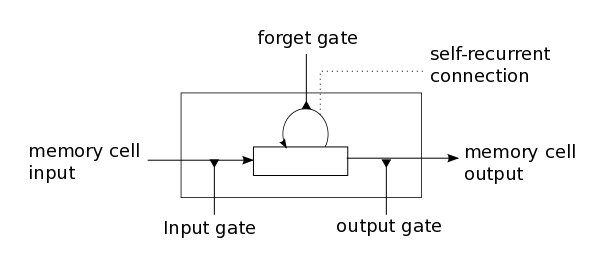
下面的公式描述了记忆元是如何在每一个时间点t来更新其状态的。在这些公式中：

  • $ x_t $ 表示在t时刻，记忆元的输入
  • $ W_i, W_f, W_c, W_o, U_f, U_c, U_o和V_o $ 表示权重矩阵
  • $ b_i, b_f, b_c 和 b_o$ 是偏好向量

首先，计算在时刻t，$i_t$，输入门和$\widetilde{C_t}$的值，其中$\widetilde{C_t}$是记忆元的期望值。
$$i_t = \sigma(W_i x_t + U_i h_{t-1} + b_i) \tag{1}$$ $$\widetilde{C_t} = tanh(W_c x_t + U_c h_{t-1} + b_c) \tag{2}$$

其次，计算$f_t$的值，其是记忆元的忘记门在时间点t的激活值。
$$f_t = \sigma(W_f x_t + U_f h_{t-1} + b_f) \tag{3}$$

给定输入门的激活值$i_t$，健忘门的激活值$f_t$和期望值$\widetilde{C_t}$, 就可以得到记忆元在时间点t的值$C_t$是。
$$ C_t = i_t * \widetilde{C_t} + f_t * C_{t-1} \tag{4} $$

得到记忆元的新的状态后，就可以计算出输出门的值，进而得到结果：
$$o_t = \sigma(W_o x_t + U_o h{t-1} + V_o C_t + b_o)\tag{5}$$ $$h_t = o_t * tanh(C_t)\tag{6}$$

本文采用的模型

在本教程中使用的模型是标准的LSTM模型的一个变种。在这个变种模型中，记忆元的输出门的激活值不依赖于记忆元的状态值$C_t$。因此，部分计算步骤效率更高（具体的计算细节请看下面的注释）。这意味着，在这个变种中，没有矩阵$V_o$，并且公式（5）被公式（7）替代。
$$o_t = \sigma(W_o x_t + U_o h_{t-1} + b_o) \tag{7}$$

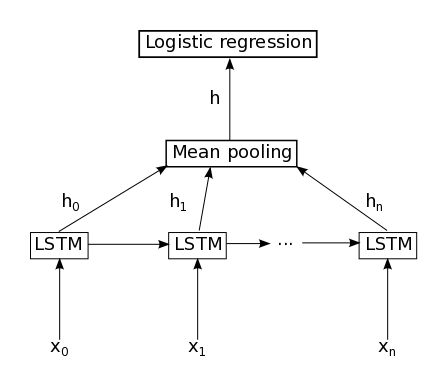
图2描述了本文所采用的模型，它由一个LSTM层加上一个平均池和logistic回归层组成。因此，给定输入序列$x_0, x_1, x_2, …, x_n$，LSTM的记忆元将计算得出表示序列$h_0, h_1, h_2, …, h_n$。表示序列取所有时间点的平均值（This representation sequence is then averaged over all timesteps resulting in representation h）。最后，这个表示值做为logistic回归层的输入，计算得到输入序列所代表的分类。

实现说明：本教程提供的代码中，公式（1），（2），（3）和（7）是并行计算的。之所以能够这样做，是因为他们不依赖于其他的公式的计算结果。具体的实现过程是，把四个矩阵$W_*$连接成一个权重矩阵W，同理，权重举证$U_*$被连接成一个矩阵U，偏好向量{b_*}被连接成一个向量b。最后，前置非线性的激活值可以通过下面公式得到。

$$z = W x_t + U h_{t-1} + b$$

然后，计算结果被分割得到i，f，$\widetilde{C_t}$和o的前置非线性激活值，并且，非线性化被独立地应用到这些变量上。（The result is then sliced to obtain the pre-nonlinearity activations for i, f, $\widetilde{C_t}$, and o and the non-linearities are then applied independently for each.）

代码 - 引用 - 联系方式

代码

LSTM的实现主要包含在以下两个文件中：

  • lstm.py: 定义和训练模型
  • imdb.py: 辅助脚本。加载和预处理IMDB数据集。

读者可以下载这些脚本并将其放在同一个目录下，然后使用下面的命令来运行：

1
THEANO_FLAGS="floatX=float32" python lstm.py

脚本会自动下载数据并解压它们。

注意：本文提供的代码中支持Stochastic Gradient Descent (SGD), AdaDelta and RMSProp的logistic回归优化方法. 建议读者使用AdaDelta或者RMSProp, 在本文提出的模型中SGD的表现非常的差。

论文

如果你使用这个教程，请引用下面这些论文
Introduction of the LSTM model:

  • pdf Hochreiter, S., & Schmidhuber, J. (1997). Long short-term memory. Neural computation, 9(8), 1735-1780.

Addition of the forget gate to the LSTM model:

  • pdf Gers, F. A., Schmidhuber, J., & Cummins, F. (2000). Learning to forget: Continual prediction with LSTM. Neural computation, 12(10), 2451-2471.

More recent LSTM paper:

  • pdf Graves, Alex. Supervised sequence labelling with recurrent neural networks. Vol. 385. Springer, 2012.

Papers related to Theano:

  • pdf Bastien, Frédéric, Lamblin, Pascal, Pascanu, Razvan, Bergstra, James, Goodfellow, Ian, Bergeron, Arnaud, Bouchard, Nicolas, and Bengio, Yoshua. Theano: new features and speed improvements. NIPS Workshop on Deep Learning and Unsupervised Feature Learning, 2012.
  • pdf Bergstra, James, Breuleux, Olivier, Bastien, Frédéric, Lamblin, Pascal, Pascanu, Razvan, Desjardins, Guillaume, Turian, Joseph, Warde-Farley, David, and Bengio, Yoshua. Theano: a CPU and GPU math expression compiler. In Proceedings of the Python for Scientific Computing Conference (SciPy), June 2010.

联系方式

对于任何的问题或反馈，请email Pierre Luc Carrier(carriepl@iro.umontreal.ca) or Kyunghyun Cho. 我们非常期望能够收到你的邮件.

参考文献

  • Hochreiter, S., & Schmidhuber, J. (1997). Long short-term memory. Neural computation, 9(8), 1735-1780.
  • Gers, F. A., Schmidhuber, J., & Cummins, F. (2000). Learning to forget: Continual prediction with LSTM. Neural computation, 12(10), 2451-2471.
  • Graves, A. (2012). Supervised sequence labelling with recurrent neural networks (Vol. 385). Springer.
  • Hochreiter, S., Bengio, Y., Frasconi, P., & Schmidhuber, J. (2001). Gradient flow in recurrent nets: the difficulty of learning long-term dependencies.
  • Bengio, Y., Simard, P., & Frasconi, P. (1994). Learning long-term dependencies with gradient descent is difficult. Neural Networks, IEEE Transactions on, 5(2), 157-166.
  • Maas, A. L., Daly, R. E., Pham, P. T., Huang, D., Ng, A. Y., & Potts, C. (2011, June). Learning word vectors for sentiment analysis. In Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies-Volume 1 (pp. 142-150). Association for Computational Linguistics.

后记

文章不长，作者写的浅显易懂，没有遇到太大的困难。当然，部分语句理解的并不透彻，术语也不是太规范。在这里赞一下vim，其中文支持比emacs 25好的太多了。